Air resistance:

Digging deeper: What is the theory behind calculating air resistance?

Now, after we understand how air resistance works and how it is applied to cycling, lets dig deeper and learn about the calculation of air resistance.

Definition of Air Resistance: The amount of resistive force air particle collision brings to the moving object.

Formula:

Understanding the formula:

1. Fd: The drag force, or air resistance. It is the force exerted by air against the motion of a moving object. Measured in Newtons(N)

2. ρ(rho): The air density of the air. This is included because density of air affects the air resistance: the denser the air is (because its cold/humid/low altitude), the bigger the drag force is, because a denser air means there are more air particles colliding with the moving object in a certain amount of area. Measured in kg/m³

3. C_d: The drag coefficient. It measures how streamlined an object is, and describes how much an object’s shape affects the drag force when an object is moving through air. It demonstrates how efficiently can air flow around the object.

Learn more about Drag Coefficient (C_d)

That’s right-to decrease air resistance, it is also possible for moving objects to decrease drag coefficient by having an aerodynamic shape that decreases drag coefficient. By having such shape, when air particles hit the object, instead of directly losing momentum and applying resistive force to the object, the air particles are now deflected because of the shape and smoothly change their directions. During this process, air particles get to keep much of their momentum, not applying them to the object, thus decreasing air resistance.

Therefore, higher drag coefficient means more air resistance and a less aerodynamic shape, and vice versa.

Fun fact: In terms of cycling, helmet manufacturers will design their helmet so it is more aerodynamic, so that the helmet decreases the drag coefficient, thereby decreasing air resistance and increasing the speed.

.

4. A: Front area that is in contact with the air particles (faces the airflow). It is measured in m².

This should be relatively easy to explain, since the greater the contact area, more air particles will collide with the moving object, and therefore will generate a stronger resistive force, and the drag increases.

5. V²: Speed (Velocity) of the moving object. It is measured in m/s or m·s⁻¹. This is also relatively easy to explain: the faster the movement of the object, the more air resistance the object faces (which is mentioned earlier), because the object will hit more air particles within a certain time range as its speed increases.

6. 1/2: 1/2 In this formula comes from the kinetic energy formula KE = 1/2 m v². This is used in the air resistance formula because the amount of momentum and energy the air particles transfer to the moving object needs to be calculated. Every air particle that collides with the moving object has a kinetic energy, and the total force the air particles produce depends directly on the kinetic energy, which is calculated by KE = 1/2 m v². Therefore, since drag force is based on kinetic energy of moving air hitting the object, and since the formula of KE includes 1/2, the formula for air resistance also must include it.

Example Calculation

A cyclist is riding their bike, moving at 10m/s. The density of the air in their region is 1.2kg/m3, the drag coefficient of the bike is 0.88, the total frontal area (human area + bike area) is 0.5m2, calculate the air resistance the cyclist faces.

Use the formula of calculating air resistance: Fd = 1/2 ρ C_d A V²

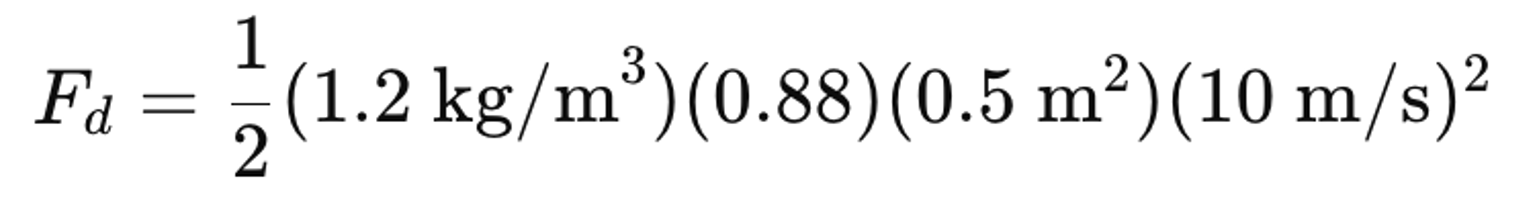
After calculation, we get: 26.4N. Therefore, the air resistance the cyclist faces is 26.4N.

Application to Cycling:

Bicycle manufacturers calculate air resistance using this formula to design bikes that are more aerodynamic and anti-air resistance, to make their bike more competitive and faster.

Using this formula, cyclists also learn to lean down when cycling, because this decreases their area facing the air flow, decreasing air resistance and increasing their speed.

Now, let's visualize air resistance using experiments